Курсовая работа: Многомерный статистический анализ в системе SPSS

Координаты центроидов по группам приведены в таблице «Функции в центроидах групп» (рис. 4.1.5). Они используются для нанесения центроидов на карту восприятия (рис. 4.1.6).

Рис. 4.1.5. Функции в центроидах групп

Рис. 4.1.6. Карта восприятия для двух дискриминантных функций D1(X) и D2(X) (* — центроид группы)

Поле «Территориальной карты» разделено дискриминантными функциями на четыре области: в левой части находятся преимущественно наблюдения четвертой группы заемщиков с очень плохими финансовыми показателями, в правой части — первой группы с отличными финансовыми показателями, в средней и нижней части — третьей и второй группы заемщиков с плохими и хорошими финансовыми показателями соответственно.

Рис. 4.1.7. Диаграмма рассеяния для всех групп

На рис. 4.1.7 приведен объединенный график распределения всех групп заемщиков вместе со своими центроидами; его можно использовать для проведения сравнительного визуального анализа характера взаимного расположения групп заемщиков банка по финансовыми показателями. В правой части графика расположены заемщики с высокими показателями, в левой — с низкой, а в средней части — со средними финансовыми показателями. Поскольку по результатам расчета вторая дискриминантная функция D2(X) оказалась незначима, то различия координат центроидов по этой оси незначительны.

Оценка кредитоспособности физических лиц в коммерческом банке

Кредитный отдел коммерческого банка провел выборочное обследование 30 своих клиентов (физических лиц). На основе предварительного анализа данных, заемщики оценивались по шести показателям (табл. 4.2.1):

Х1 — заемщик брал кредит в коммерческих банках ранее;

Х2 — среднемесячный доход семьи заемщика, тыс. руб.;

Х3 — срок (период) погашения кредита, лет;

Х4 — размер выданного кредита, тыс. руб.;

Х5 — состав семьи заемщика, чел.;

Х6 — возраст заемщика, лет.

При этом по вероятности возврата кредита выявлены три группы заемщиков:

-   Группа 1 — с низкой вероятностью погашения кредита;

-   Группа 2 — со средней вероятностью погашения кредита;

-   Группа 3 — с высокой вероятностью погашения кредита.

Требуется:

На основе дискриминантного анализа с использованием пакета SPSS необходимо классифицировать трех клиентов банка (по вероятности погашения кредита), т.е. оценить принадлежность каждого из них к одной из трех групп. По результатам расчета построить значимые дискриминантных функции, их значимость оценить по коэффициенту Уилкса (λ). В пространстве двух дискриминантных функций для каждой группы построить диаграммы взаимного расположения наблюдений и объединенную диаграмму. Оценить место расположения каждого заемщика на этих диаграммах. Выполнить интерпретацию результатов проведенного анализа.

Таблица 4.2.1. Исходные данные

Ход выполнения:

Для построения дискриминантного анализа в качестве зависимой переменной выберем вероятность своевременного погашения кредита клиентом. Учитывая, что она может быть низкой, средней и высокой, каждой категории присвоим соответствующую оценку 1,2 и 3.

Ненормированные канонические коэффициенты дискриминантных функций, приведенные на рис. 4.2.1, используются для построения уравнения дискриминантных функций D1(X), D2(X):

1.) D1(X) =

2.) D2(X) =

Рис. 4.2.1. Коэффициенты канонической дискриминантной функции

Рис. 4.2.2. Лямбда Уилкса

По коэффициенту Уилкса (рис. 4.2.2) для второй функции значимость более 0.001, следовательно, ее для дискриминации использовать нецелесообразно.

Данные таблицы «Результаты классификации» (рис. 4.2.3) свидетельствуют о том, что для 93,3 % наблюдений классификация проведена корректно, высокая точность достигнута в первой и второй группах (100% и 91,7%), менее точные результаты получены в третьей группе (88, 9%).

Рис. 4.2.3. Результаты классификации

Информация о фактических и предсказанных группах для каждого клиента приведены в таблице «Поточечные статистики» (рис. 4.2.4).

В результате дискриминантного анализе высокой вероятностью определена принадлежность новых клиентов банка к обучающему подмножеству М3 – первый, второй и третий клиент (порядковый номера 31, 32, 33) отнесены к подмножеству М3 с соответствующими вероятностями 99%, 99% и 100%.

Рис. 4.2.4. Поточечная статистика

Рис. 4.2.5. Функции в центроидах групп

Координаты центроидов по группам приведены в таблице «Функции в центроидах групп» (рис. 4.2.5). Они используются для нанесения центроидов на карту восприятия (рис. 4.2.6).

Поле «Территориальной карты» разделено дискриминантными функциями на три области: в левой части находятся преимущественно наблюдения первой группы клиентов с очень низкой вероятностью погашения кредита, в правой части — третьей группы с высокой вероятностью, в средней — второй группы клиентов со средней вероятностью возврата кредита соответственно.

На рис. 4.2.7 (а – в) отражено расположение клиентов каждой из трех групп на плоскости двух дискриминантных функций D1(X) и D2(X). По этим графикам можно проводить детальный анализ вероятности погашения кредита внутри каждой группы, судить о характере распределения клиентов и оценивать степень их удаленности от соответствующего центроида.

Рис. 4.2.6. Карта восприятия для трех дискриминантных функций D1(X) и D2(X) (* — центроид группы)

Так же на рис. 4.2.7 (г) в той же системе координат приведен объединенный график распределения всех групп клиентов вместе со своими центроидами; его можно использовать для проведения сравнительного визуального анализа характера взаимного расположения групп клиентов банка с разными вероятностями погашения кредита. В левой части графика расположены заемщики с высокой вероятностью погашения кредита, в правой — с низкой, а в средней части — со средней вероятностью. Поскольку по результатам расчета вторая дискриминантная функция D2(X) оказалась незначима, то различия координат центроидов по этой оси незначительны.

б)

г)

а)

в)

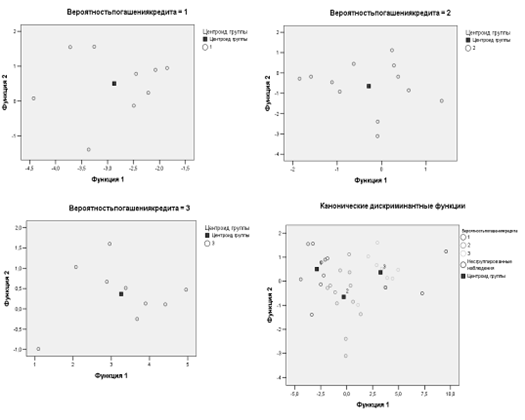
Рис. 4.2.7. Расположение наблюдений на плоскости двух дискриминантных функций для групп с низкой (а), средней (б), высокой (с) вероятностью погашения кредита и для всех групп (г)

Список литературы

1.  «Многомерный статистический анализ в экономических задачах. Компьютерное моделирование в SPSS», Вузовский учебник, 2009 г.

2.  Орлов А.И. «Прикладная статистика» М.: Издательство «Экзамен», 2004

3.  Фишер Р.А. «Статистические методы для исследователей», 1954 г.

4.  Калинина В.Н., Соловьев В.И. «Введение в многомерный статистический анализ» Учебное пособие ГУУ,2003;

5.  Ахим Бююль, Петер Цёфель, «SPSS: искусство обработки информации» Изд-во DiaSoft, 2005г.;

6.  http://ru.wikipedia.org/wiki