
 |
|
|
Реферат: Способы улучшения цифровых сигналов в условиях ограниченного объема априорной информацииРеферат: Способы улучшения цифровых сигналов в условиях ограниченного объема априорной информацииСодержание Основная часть Выводы Библиографический список В современных радиоэлектронных системах в процессе передачи сигнала на него накладываются различные шумы. Процесс приема и перевода сигнала в цифровой вид также сопряжен с внесением в сигнал шумовой составляющей. В большинстве случаев шум является аддитивным. Как правило, при обработке сигнала основной задачей является выделение полезной и ослабление шумовой составляющей. Для решения данной задачи чаще всего используются критерий минимума среднеквадратической погрешности или критерий среднеабсолютного отклонения. В связи с чем актуальной является задача обработки цифрового сигнала одновременно по нескольким критериям [1]. В связи с этим значительный интерес представляет использование многокритериальных методов обработки результатов измерений, представленных единственной реализацией при ограниченном объеме априорной информации о функциях полезной составляющей и шуме. Цель работы – уменьшение дисперсии шумовой составляющей многокритериальными методами сглаживания входного сигнала, представленного единственной реализацией нестационарного случайного процесса в условиях априорной неопределенности. Пусть исходные результаты измерений представляют собой дискретную
последовательность значений измеряемой физической величины
где Функциональная зависимость от времени Получение оценки
а также (или) уменьшения суммы квадратов конечных разностей второго порядка:
При этом в качестве меры расхождения исходного и полезного сигналов используется сумма:
Для определения оценок
а также минимизаций трехкритериальной целевой функцией вида:
где Заметим, что целевые функции (6, 5–7) непрерывны и ограничены
снизу на множестве
то есть следующей системе
Перепишем систему (9) в виде:
Докажем, что система уравнений (10) имеет единственное решение.
С этой целью методом математической индукции установим справедливость
утверждения
где Итак, утверждения Таким образом, система уравнений (5) имеет единственное решение; аналогично доказательство единственности решения для целевых функций вида (6) и (7). Для нахождения точки наименьшего значения целевых функций Для целевой функции (6), получим:
Целевая функция (7) сводится к решению системы:
Кроме того, для целевой функции вида (5) введем величину:
Для целевой функции вида (6) – величину:
Для целевой функции вида (7) – величину:
Если – для целевой функции вида (5):
– для целевой функции вида (6):
– для целевой функции вида (7):
Так как в точке
После этого проверяем условие
Если неравенство (19) выполняется, требуемая точность
считается достигнутой, и расчет заканчивается. Тогда Таким образом, вектор оценок Также в работе предложено аналитическое решение двухкритериальной целевой функции вида (5). Как установлено ранее, точка минимума функции (5) является единственным решением системы линейных уравнений [2, 3]
Покажем, что это решение имеет вид
где
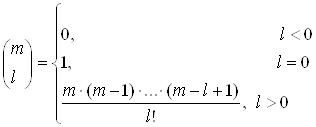 – биноминальные – биноминальные
Воспользовавшись соотношениями (21), (22) при
Подставив результат в первое уравнение (20), получим тождество
Убедимся в том, что величины (21) (при условиях (22)–(24))
удовлетворяют k-му уравнению системы (20) и при
где Преобразуем левую часть уравнения:
Упростим часть выражения в левой части, используя свойства биномиальных коэффициентов [4]:
(здесь и далее считаем, что при Таким образом, k-е уравнение системы (20) принимает вид
С учетом выражений (23) и (25) полученное соотношение перепишется следующим образом:
Упростим левую часть уравнения, используя свойства биноминальных коэффициентов:
Преобразуем коэффициент при
Таким образом, k-е уравнение системы (20) превращается в тождество
Докажем, что величины (21) удовлетворяют
или
Коэффициент при
Уравнение принимает вид
Выражение в скобках равно
Так как Итак, выражение (21) (при подстановке в него выражений (22)–(24)) дает единственное решение системы уравнений (20); это решение минимизирует функцию (5), и других точек минимума данная функция не имеет. Для проверки эффективности многокритериальных методов сглаживания цифровых сигналов в качестве критерия используем среднеквадратическое отклонение оценок от значений входной реализации:
На рис. 1 представлены кривые
среднеквадратического отклонения, полученные при обработке двухкритериальной
целевой функцией, при точном решении и при итерационном. В качестве полезной
составляющей использовалась функция, огибающая которой описывается параболой,
среднеквадратическое отклонение шума
Рис. 1. Зависимость Анализ результатов, представленных на рис. 1, позволяет сделать вывод, что результаты оценки эффективности, полученные при решении целевой функции (5) итерационным алгоритмом и при определении точного решения, практически совпадают, разброс параметров составляет менее 1 % [5]. Таким образом, на основе проведенных исследований получены аналитические выражения для минимизации многокритериальной целевой функции, в условиях ограниченного объема априорной информации о функции сигнала, статистических характеристиках шума и ограниченности объема выборки. На рис. 2 представлен алгоритм получения оценок многокритериальными методами сглаживания сигналов, основанных на целевых функциях (5), (6,6) и (6,7), в условиях ограниченного объема априорной информации.
Рис. 2. Алгоритм вычисления оценок многокритериальными методами сглаживания сигналов Используя полученный алгоритм, удалось реализовать метод сглаживания сигналов на основе компьютерной программы для выполнения машинного моделирования (свидетельства об официальной регистрации программы для ЭВМ, РОСПАТЕНТ: № 2006612520, № 2007612944, № 2008611151). Для нахождения импульсной характеристики используем соотношения (21)–(24), т.е. отклика системы на единичный импульс [6]:
где Имеем
или
На рис. 3 представлены графики обработки входной реализации,
представленные единичным импульсом (26), на основе выражения (27), при условии
Рис. 3. обработка
целевой функцией входной реализации единичной амплитуды, параметры Анализ зависимостей, представленных на рис. 3, показывает,
что импульсная характеристика лежит только в положительной полуплоскости.
Следует отметить, что импульсная характеристика быстро спадает, в связи с этим
можно ее ограничить и рассматривать на интервале На рис. 4 представлены нормированные значения результатов, полученных
ранее для проведения сравнения величины
Рис. 4. Сравнение нормированных характеристик при Анализ нормированных импульсных характеристик, представленных
на рис. 4, показывает, что при увеличении параметра Для обработки цифровых сигналов по мере поступления данных
предлагается обработка входной реализации путем нахождения оценок
многокритериальной целевой функции в задаваемом окне Выбор величины окна обработки обусловлен минимумом итерационных
затрат для получения оценок входной реализации и представлен на рис. 5 при а)
б) Рис. 5. График изменения значения среднеквадратического отклонения от ширины окна (а) и величины шага перемещения окна (б) Анализ результатов, представленных на
рис. 5, показал, что минимум зависимости
Рис. График выбора параметра Анализ результатов, представленных на рис. 6, показал, что
использование двухкритериальной целевой функции вида (6) позволяет локализовать
значение параметра В табл. 1 приведены значения параметра Таблица 1 Минимальная среднеквадратическая погрешность
Процесс получения оценок в скользящем окне параметра
где На рис. 7 представлен пример обработки цифрового сигнала
Рис. 7. Пример сглаживания цифрового сигнала при наличии импульсных помех с последующим прогнозированием цифровой сигнал шум априорная выводы 1. Разработаны и исследованы многокритериальные методы сглаживания цифровых сигналов в условиях ограниченного объема априорной информации о функциях сигнала и статистических характеристиках шума. 2. Использование многокритериальных методов сглаживания для обработки цифровых сигналов в скользящем окне, показало их высокую эффективность, в среднем на 25 %, в сравнении с обработкой всей реализации. При наличии во входной реализации функций разрыва первого рода или скачков единичной амплитуды происходит повышение эффективности в среднем на 60 %, в сравнении с используемыми на практике аналогами, в качестве критерия эффективности используется среднеквадратическое отклонение оценок от значений входной реализации. Библиографический список 1. Марчук В.И. Сравнение результатов решений двухкритериальных целевых функций. / В.И. Марчук, Е.А. Семенищев // Наука и образование без границ: материалы 3-й междунар. научно-практич. конф. Т. 1 Технология. – София : «Бял ГРАД-БГ» ООД, 2007. – С. 80–82. 2. Марчук В.И. Двухкритериальный метод обработки результатов измерений / В.И. Марчук, К.Е. Румянцев, И.С. Шрайфель // Авиакосмическое приборостроение. – 2008. – № 12. – С. 33–35. 3. Практические аспекты цифровой обработки сигналов (Practical aspects of digital signal processing) : монография / под ред. В.И. Марчука. – Шахты : Изд-во ЮРГУЭС, 2007. – 207 с. 4. Корн Г. Справочник по математике (для научных работников и инженеров) / Г. Корн, Т. Корн. – М., 2007. – 832 с. : ил. 5. Семенищев Е.А. Исследование эффективности итерационного метода выделения полезного сигнала на основе двухкритериальной целевой функции / Е.А. Семенищев // Цифровая обработка сигналов и ее применение: сб. тр. Российского научно-технического общества радиотехники, электроники и связи имени А.С. Попова. – М., 2008. – Вып. X-1. – С. 452–455. 6. Марчук В.И. Исследование решения двухкритериальной целевой функции / В.И. Марчук, Е.А. Семенищев, А.И. Шерстобитов // Информационные технологии в современном мире : материалы междунар. конф. – Таганрог : ТРТУ, 2009 – Ч. 2. – С. 93. 7. Марчук В.И. Исследование зависимостей параметров двухкритериального метода при обработке в скользящем окне / В.И. Марчук, Е.А. Семенищев // Информация, сигналы, системы: вопросы методологии, анализа и синтеза : материалы междунар. научно-практич. конф. – Таганрог : Изд-во ТТИ ЮФУ, 2008. – ч. 4. – С. 45–47. 8. Марчук В.И. Исследование двухкритериальной целевой функции для обработки цифровых рядов в реальном масштабе времени / В.И. Марчук, Е.А. Семенищев // Современные методы и средства обработки пространственно-временных сигналов : сб. статей VI всероссийской научно-технич. конф. – Пенза, 2008. – С. 568. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||
| НОВОСТИ |  |
|
 |
||
| ВХОД |  |
|
|
|||||
Рефераты бесплатно, реферат бесплатно, курсовые работы, реферат, доклады, рефераты, рефераты скачать, рефераты на тему, сочинения, курсовые, дипломы, научные работы и многое другое. |
||
При использовании материалов - ссылка на сайт обязательна. |
||